Ishani Karmarkar

I am currently a PhD student at Stanford University. My research primarily focuses on problems at the intersection of optimization, machine learning, and algorithm design. I am very fortunate to be advised by Aaron Sidford and Ellen Vitercik.

Previously, I earned a BS in Applied and Computational Mathematics with a Minor in Computer Science from the California Institute of Technology (Caltech), where I did undergraduate research with Bamdad Hosseini and Andrew Stuart.

I can be reached at ishanik[at]stanford[dot]edu.

Publications

Please note: in my field (theory) authors are always listed alphabetically by last name!

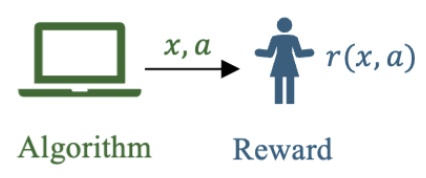
Active Learning for Stochastic Contextual Linear Bandits

Prior algorithms for stochastic contextual banditys strategically sample actions but naively (passively) sampling contexts from the underlying context distribution. But in many practical scenarios—including online content recommendation, survey research, AI alignment, and clinical trials—practitioners can actively sample or recruit contexts based on prior knowledge of the contexts. Despite this potential for active learning, strategic context sampling in stochastic contextual bandits is underexplored. We propose an algorithm that learns a near-optimal policy by strategically sampling rewards of context-action pairs. We prove it enjoys improved instance-dependent guarantees and demonstrate empirically that our algorithm reduces the number of samples needed to learn a near-optimal policy.

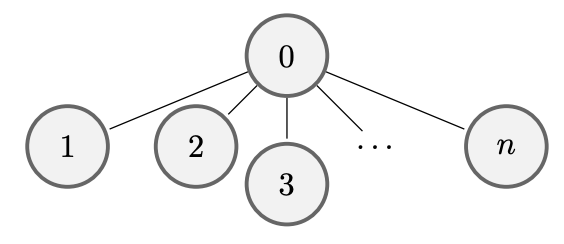
Mean-Field Sampling for Cooperative Multi-Agent Reinforcement Learning

Designing efficient algorithms for multi-agent reinforcement learning (MARL) is fundamentally challenging because the size of the joint state and action spaces grows exponentially in the number of agents. These difficulties are exacerbated when balancing sequential global decision-making with local agent interactions. In this work, we propose a new algorithm and a decentralized randomized policy for a system with $n$ agents. For any $k\leq n$, our algorithm learns a policy for the system in time polynomial in $k$. We prove that this learned policy converges to the optimal policy on the order of $\smash{\tilde{O}(1/\sqrt{k})}$ as the number of subsampled agents $k$ increases. (arxiv)

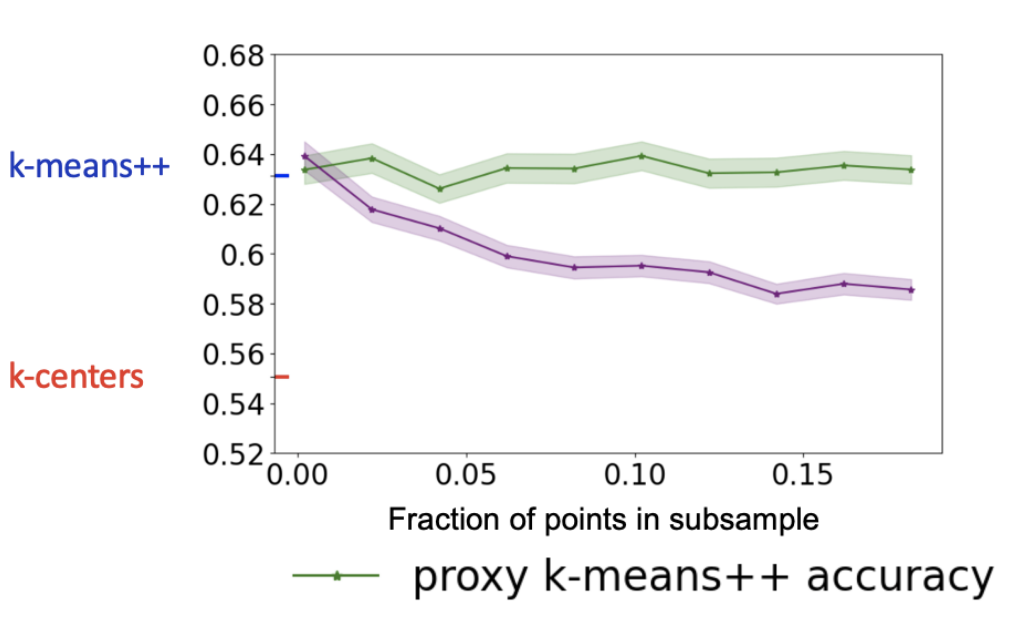
Accelerating data-driven algorithm selection for combinatorial partitioning problems

Data-driven algorithm selection is an approach for choosing effective heuristics for computational problems. It operates by evaluating a set of candidate algorithms on a collection of representative training instances and selecting the one with the best empirical performance. However, running each algorithm on every training instance is computationally expensive, making scalability a central challenge. A practical workaround is to evaluate algorithms on smaller proxy instances derived from the original inputs. We provide the first theoretical foundations for this practice by formalizing the notion of size generalization: predicting an algorithm’s performance on a large instance by evaluating it on a smaller, representative instance, subsampled from the original instance. We provide size generalization guarantees for several clustering algorithms and max-cut algorithms.

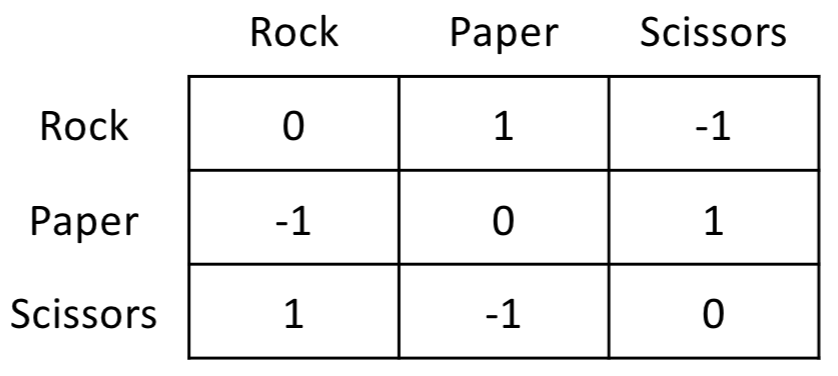
Solving Zero-Sum Games with Fewer Matrix-Vector Products

We study the fundamental problem of computing an approximate Nash equilibrium of a two-player zero-sum game given access to only a small number of matrix-vector products. We provide the first algorithm that provably converges to an $\epsilon$-approximate Nash equilibrium in $\tilde{O}(\epsilon^{-8/9})$ matrix-vector products, which is the first improvement on this problem since Nemerovski’s and Nesterov’s algorithms two decades ago. Our techniques also yield improved rates for other applications, such as the problem of computing a hard-margin SVM (linear classifier) and certain generalizations for linear regression. (arxiv)

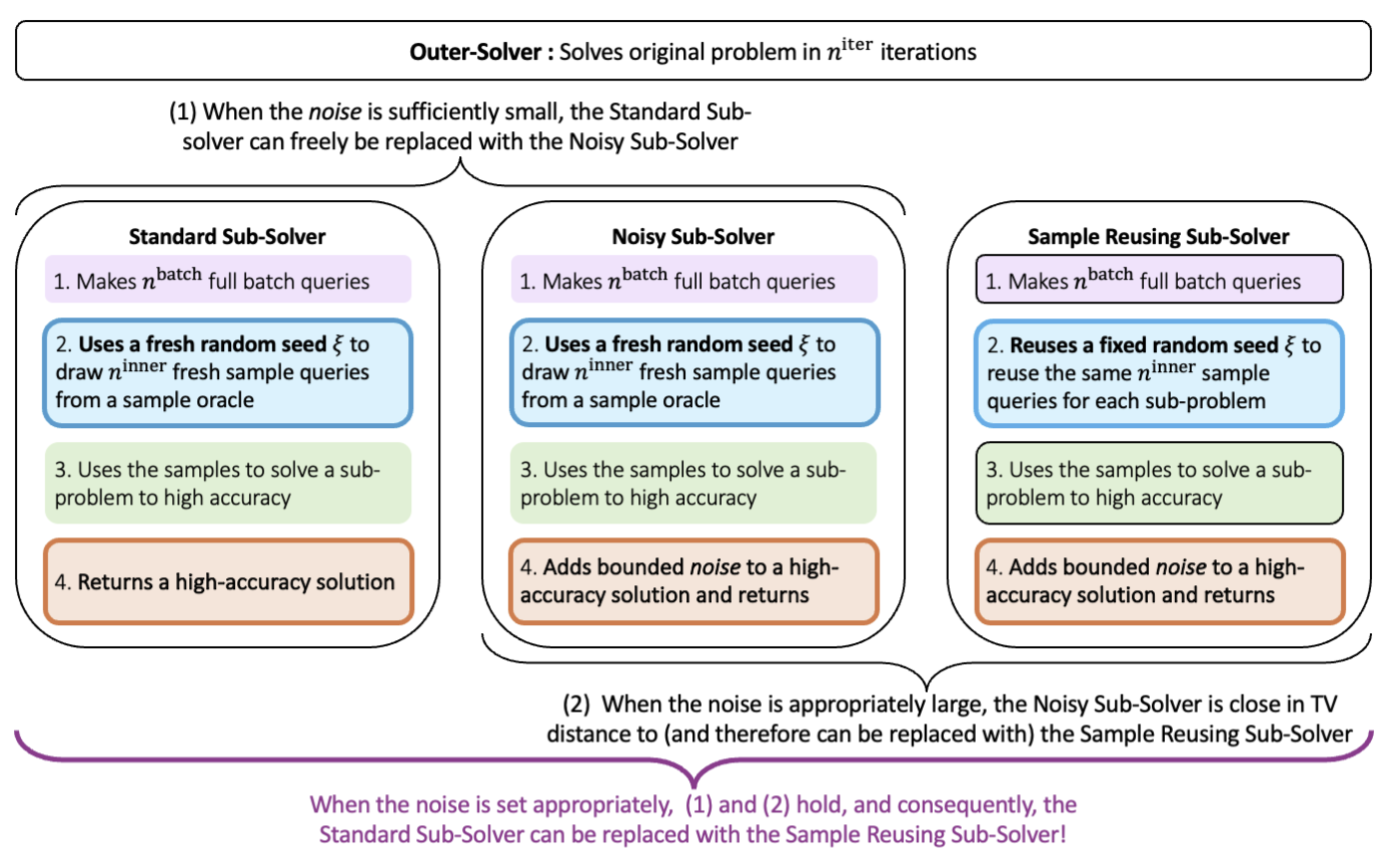
Reusing Samples in Variance-Reduction

We provide a general framework to improve trade-offs between the number of full batch and sample queries used to solve structured optimization problems. Our results apply to a broad class of randomized optimization algorithms that iteratively solve sub-problems to high accuracy. We show that such algorithms can be modified to _reuse the randomness used to query the input across sub-problems. Consequently, we improve the trade-off between the number of gradient (full batch) and individual function (sample) queries for finite sum minimization, the number of matrix-vector multiplies (full batch) and random row (sample) queries for top-eigenvector computation, and the number of matrix-vector multiplies with the transition matrix (full batch) and generative model (sample) queries for optimizing Markov Decision Processes.

Truncated Variance-Reduced Value Iteration

We study the problem of solving a discounted MDP with a generative model, a fundamental and extensively studied reinforcement learning setting. We present a new randomized variant of value iteration that improves the runtime for computing a coarse optimal solution. Importantly, our method is model-free and takes a step towards improving the sample efficiency gap between model-based and model-free methods in this setting. (arxiv)

Faster Spectral Density Estimation and Sparsification in the Nuclear Norm

Spectral Density Estimation (SDE) is the problem of efficiently learning the distribution of eigenvalues of a graph and has broad applications in computational science and network science. In this paper, we present new fast and simple randomized and deterministic algorithms for spectral density estimation via a new notion of graph sparsification, which we call nuclear sparsification. (arxiv)

Towards Optimal Effective Resistance Estimation

Computing the effective resistance of nodes in a network (or, undirected graph) is a fundamental task with many applications, for instance, in graph machine learning, graph data analysis, and the design of efficient graph algorithms. In this paper we introduce new efficient algorithms for estimating effective resistances in well-connected graphs. We also prove improved time lower bounds for effective resistance estimation. In addition, we provide natural extensions of our work to related problems on symmetric diagonally dominant (SDD) and positive semi-definite (PSD) matrices. (arxiv)

Real-bogus classification for the Zwicky Transient Facility using deep learning

In this project, we present a convolutional neural network classifier for classifying real versus bogus data in astronomical images from the Zwicky Transients Facility (ZTF), a new robotic time-domain astronomical survey. (arxiv)

Design and source code from Jon Barron's website